In this post I'll introduce group homology and cohomology. The main reference for this entry will be Kenneth Brown's 'Cohomology of Groups'.
Background Definitions
Definition: Let $R$ be a ring and let $M$ be an $R$-module. A resolution of $M$ is an exact sequence of $R$-modules $$\cdots \rightarrow F_2 \rightarrow F_1 \rightarrow F_0 \rightarrow M \rightarrow 0.$$ We denote such a resolution $$F_\bullet \rightarrow M \rightarrow 0.$$
Recall the definition of a projective module:
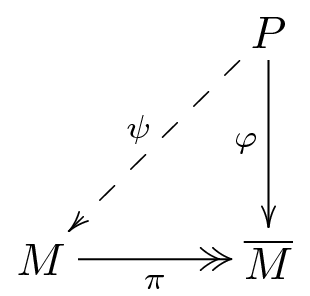
Definition: Let $P$ be an $R$-module. P is called projective if whenever we have $R$-modules $M$ and $\overline{M}$ with maps $\varphi : P \rightarrow \overline{M}$ and $\pi : M \twoheadrightarrow \overline{M}$, we can construct a map $\psi : P \rightarrow M$ such that $\varphi = \pi \circ \psi$.
Definition: A free resolution of an $R$-module $M$ is a resolution $F_\bullet \rightarrow M \rightarrow 0$ of $M$ such that if $i \in \mathbb{Z}_{\geq 0}$ then $F_i$ is free. A projective resolution of $M$ satisfies $F_i$ projective for $i \in \mathbb{Z}_{\geq 0}$.
Theorem: Let $R$ be a ring and let $M$ be an $R$-module. If $M$ is free then $M$ is projective.
We now state two important properties of resolutions which allow us to use them for the construction of group homology.
Theorem: Let $R$ be a ring and let $M$ be an $R$-module. Then a free resolution $F_\bullet \rightarrow M \rightarrow 0$ exists.
Theorem: Let $F_\bullet \rightarrow M \rightarrow 0$ and $G_\bullet \rightarrow M \rightarrow 0$ be two projective resolutions of an $R$-module $M$, these are then homotopic.
Definition: Let $M$ be a $\mathbb{Z} G$-module. The group of co-invariants of $M$ is $$M_G := M / \left< \{ (gm - m) \, | \, g \in G, m \in M \} \right>.$$
$M_G$ is the largest quotient of $M$ on which $G$ acts trivially. One can think of $M_G$ as being $M$ divided out by the $G$-action. Further, it is also true that $M_G \cong \mathbb{Z} \otimes_{\mathbb{Z} G} M$.
Group Homology with Trivial Coefficients
Definiton: Let $G$ be a group and let $P_\bullet \rightarrow \mathbb{Z} \rightarrow 0$ be a projective resolution of $\mathbb{Z} G$-modules. Then the group homology of $G$ is defined to be $$H_* G := H_* ((P_\bullet)_G),$$ where $(P_\bullet)_G$ is defined to be the complex $$\cdots \rightarrow (P_2)_G \rightarrow (P_1)_G \rightarrow (P_0)_G.$$
Example: Let $n \in \mathbb{Z}_{> 0}$ and let $G = \mathbb{Z} / n$. We take $g \in G$ such that $\left< g \right> = G$ and let $N = 1 + g + g^2 + \cdots + g^{n - 1}$, the 'norm element'. A projective resolution is then $$\cdots \xrightarrow{g - 1} \mathbb{Z} G \xrightarrow{N} \mathbb{Z} G \xrightarrow{g - 1} \mathbb{Z} G \xrightarrow{aug} \mathbb{Z} \rightarrow 0,$$ where $aug : \mathbb{Z} G \rightarrow \mathbb{Z}$ is the augmentation map, ie $$aug(\alpha_0 + \alpha_1 g + \alpha_2 g^2 + \cdots \alpha_{n - 1} g^{n - 1}) = \sum_{i = 0}^{n - 1} \alpha_i.$$ We then look at the corresponding $(P_\bullet)_G$ complex, noting that since $G$ acts trivially on $(P_\bullet)_G$, $g$ will correspond to the action of $1$ on the complex: $$\cdots \xrightarrow{1 - 1 = 0} \mathbb{Z} \xrightarrow{1+1+\cdots+1 = n} \mathbb{Z} \xrightarrow{0} \mathbb{Z}.$$ Then taking the homology of this complex we find that $$H_* G = \left\{ \begin{array}{l l} \mathbb{Z}, & * = 0,\\ \mathbb{Z} / n, & * \text{ odd},\\ 0, & * > 0, * \text{ even}. \end{array} \right.$$
Group Homology with Coefficients
Definition: Let G be a group and let $P_\bullet \rightarrow \mathbb{Z} \rightarrow 0$ be a projective resolution of $\mathbb{Z} G$-modules. Let $M$ be a $\mathbb{Z} G$-module. Then the homology of $G$ with coefficients in $M$ is defined to be $$H_* (G; M) := H_* (P_\bullet \otimes_{\mathbb{Z} G} M),$$ where $P_\bullet \otimes_{\mathbb{Z} G} M$ is the complex $$\cdots \rightarrow P_2 \otimes_{\mathbb{Z} G} M \rightarrow P_1 \otimes_{\mathbb{Z} G} M \rightarrow P_0 \otimes_{\mathbb{Z} G} M.$$
We should note straight away that in the case where we're working with trivial coefficients (that is $M = \mathbb{Z}$), we get that $$H_* (G; \mathbb{Z}) = H_* (P_\bullet \otimes_{\mathbb{Z} G} \mathbb{Z}) = H_* (P_\bullet)_G.$$
Example: We will calculate $H_* (\mathbb{Z} / 2; M)$ where $M = \mathbb{Z}$ and $\mathbb{Z} / 2$ acts on $M$ by multiplication by $\pm 1$. We will write $H_* (\mathbb{Z} / 2; M)$ throughout to avoid confusion with the trivial $\mathbb{Z} / 2$-module. Let $g$ be the generator of $\mathbb{Z} / 2$, then $g \in \mathbb{Z} / 2$ acts as multiplication by $-1$ on $M$ and $1 \in \mathbb{Z} / 2$ acts as multiplication by $+1$ on $M$. Using the example above, we have the following projective resolution $$\cdots \xrightarrow{g - 1} \mathbb{Z} G \xrightarrow{g + 1} \mathbb{Z} G \xrightarrow{g - 1} \mathbb{Z} G \xrightarrow{aug} \mathbb{Z} \rightarrow 0,$$ with $aug$ the augmentation map defined above. Then, looking at $P_\bullet \otimes_{\mathbb{Z} G} M$ we get the complex $$\cdots \xrightarrow{g - 1} \mathbb{Z} G \otimes_{\mathbb{Z} G} M \xrightarrow{g + 1} \mathbb{Z} G \otimes_{\mathbb{Z} G} M \xrightarrow{g - 1} \mathbb{Z} G \otimes_{\mathbb{Z} G} M,$$ which becomes $$\cdots \xrightarrow{-1 - 1 = -2} M \xrightarrow{1 - 1 = 0} M \xrightarrow{-2} M.$$ Calculating the homology of the resulting complex gives us the following: $$H_* (\mathbb{Z} / 2; M) = \left\{ \begin{array}{l l} \mathbb{Z} / 2, & * \text{ even},\\ 0, & * \text{ odd}. \end{array} \right.$$
Example: Now we'll look at $H_* (\mathbb{Z} / n; \mathbb{C})$ where $\mathbb{Z} / n$ acts on $\mathbb{C}$ as multiplication by an $n$th root of unity. That is, let $\zeta = e^{\frac{2 \pi i}{n}}$ and let $g \in \mathbb{Z} / n$ such that $\left< g \right> = \mathbb{Z} / n$, then $g$ acts on $\mathbb{C}$ as multiplication by $\zeta$. Again, our projective resolution is $$\cdots \xrightarrow{g - 1} \mathbb{Z} G \xrightarrow{N} \mathbb{Z} G \xrightarrow{g - 1} \mathbb{Z} G \xrightarrow{aug} \mathbb{Z} \rightarrow 0,$$ with $aug$ the augmentation map and $N$ the norm element above. Looking at the complex $P_\bullet \otimes_{\mathbb{Z} G} \mathbb{C}$ gives us $$\cdots \xrightarrow{g - 1} \mathbb{C} \xrightarrow{N} \mathbb{C} \xrightarrow{g - 1} \mathbb{C}.$$ Now, looking at the maps, the action of $g - 1$ on $\mathbb{C}$ is multiplitation by $\zeta - 1$ which is a bijection on $\mathbb{C}$, and the action of $N = 1 + g + g^2 + \cdots + g^{n - 1}$ is multiplication by $1 + \zeta + \zeta^2 + \cdots + \zeta^{n - 1} = 0$ since it is the sum of all the $n$th roots of unity. Thus our complex becomes: $$\cdots \xrightarrow{\zeta - 1} \mathbb{C} \xrightarrow{0} \mathbb{C} \xrightarrow{\zeta - 1} \mathbb{C}.$$ Calculating the homology of this complex then gives us that $H_* (\mathbb{Z} / n; \mathbb{C}) = 0$.
This last example is a result of the following proposition:
Proposition: Let $H \subset G$ be a finite index subgroup, let $M$ be a $\mathbb{Z} G$-module and let $n \in \mathbb{Z}_{\geq 0}$. If $H_i (H; M) = 0$ then $H_i (G; M)$ is annihilated by $[G : H]$. Furthermore, if $[G : H]$ is invertible in $M$ then $H_i (G; M) = 0$.
Clearly $1 \subset \mathbb{Z} / n$ is a finite index subgroup with $[1 : \mathbb{Z} / n] = n$ which is invertible in $\mathbb{C}$. Now if $i \in \mathbb{Z}_{> 0}$ we have that $H_i (1; \mathbb{C}) = 0$, which leads us to the conclusion that if $i \in \mathbb{Z}_{> 0}$ then $H_i (\mathbb{Z} / n; \mathbb{C}) = 0$. Indeed, if $G$ is any finite group then the same argument will give us that $H_i (G; \mathbb{C}) = 0$ for $i \in \mathbb{Z}_{\geq 0}$.
Group Cohomology with Coefficients
Definition: Let $R$ be a ring and let $C$ and $C'$ be two chain complexes of $R$-modules. Define the set of degree $n$, graded $R$-module homomorphisms from $C$ to $C'$ to be $$\mathcal{Hom}_R (C, C')_n := \prod_{q \in \mathbb{Z}} Hom_R (C_q, C_{q + n}').$$ Define the boundary operator $$\begin{align*}D_n : \mathcal{Hom}_R (C, C')_n &\rightarrow \mathcal{Hom}_R (C, C')_{n - 1}\\ f &\mapsto d' \circ f - (-1)^n f \circ d.\end{align*}$$ The complete complex $\mathcal{Hom}_R (C, C')$ is called the function complex from $C$ to $C'$, that is $$\cdots \xrightarrow{D_{n + 2}} \mathcal{Hom}_R (C, C')_{n + 1} \xrightarrow{D_{n + 1}} \mathcal{Hom}_R (C, C')_{n} \xrightarrow{D_{n}} \mathcal{Hom}_R (C, C')_{n - 1} \xrightarrow{D_{n - 1}} \cdots.$$ We can think of this function complex as a cochain complex by setting $$\mathcal{Hom}_R (C, C')^n := \mathcal{Hom}_R (C, C')_{-n},$$ similarly for $D^n$, giving us the cochain complex: $$\cdots \xrightarrow{D^{n - 2}} \mathcal{Hom}_R (C, C')^{n - 1} \xrightarrow{D^{n - 1}} \mathcal{Hom}_R (C, C')^{n} \xrightarrow{D^{n}} \mathcal{Hom}_R (C, C')^{n + 1} \xrightarrow{D^{n + 1}} \cdots.$$
Definition: Let G be a group and let $P_\bullet \rightarrow \mathbb{Z} \rightarrow 0$ be a projective resolution of $\mathbb{Z} G$-modules. Let $M$ be a $\mathbb{Z} G$-module. Then the cohomology of $G$ with coefficients in $M$ is defined to be $$H^* (G; M) := H^* (\mathcal{Hom}_{\mathbb{Z} G} (P_\bullet, M)),$$ where $M$ is regarded as the chain complex with $M$ in dimension $0$ and $0$ in all non-zero dimensions.
Example: Let $m \in \mathbb{Z}_{> 0}$, let $G = \mathbb{Z} / m$ and take $g \in G$ such that $\left< g \right> = G$. We will calculate $H^* (\mathbb{Z} / m ; \mathbb{Z})$, where $g$ acts on $\mathbb{Z}$ by the trivial action (that is $g$ acts by $1$). As above, a projective resolution of $\mathbb{Z}$ is, $$\cdots \xrightarrow{g - 1} \mathbb{Z} G \xrightarrow{N} \mathbb{Z} G \xrightarrow{g - 1} \mathbb{Z} G \xrightarrow{aug} \mathbb{Z} \rightarrow 0,$$ with $aug : \mathbb{Z} G \rightarrow \mathbb{Z}$ the augmentation map and $N : \mathbb{Z} G \rightarrow \mathbb{Z} G$ the norm map as defined above. Looking at the definition of $\mathcal{Hom}_{\mathbb{Z} G} (P_\bullet, \mathbb{Z})$, we see that $$\mathcal{Hom}_{\mathbb{Z} G} (P_\bullet, \mathbb{Z})_n := \prod_{q \in \mathbb{Z}} Hom_{\mathbb{Z} G} ((P_\bullet)_q, (\mathbb{Z})_{n + q}).$$ Then, noting that if $n \neq -q$ we get $(\mathbb{Z})_{n + q} = 0$, we find that for $q \geq 0$, $$\begin{align*} Hom_{\mathbb{Z} G} ((P_\bullet)_q, (\mathbb{Z})_{n + q} ) &= Hom_{\mathbb{Z} G} (\mathbb{Z} G, (\mathbb{Z})_{n + q})\\ &= \left\{ \begin{array}{l l} \mathbb{Z}, & n = -q,\\ 0, & n \neq -q. \end{array}\right. \end{align*}$$ This leads us to the conclusion that for $n \in \mathbb{Z}$, $$\mathcal{Hom}_{\mathbb{Z} G} (P_\bullet, \mathbb{Z} ) = \left\{ \begin{array}{l l} \mathbb{Z}, & n \leq 0,\\ 0, & n > 0. \end{array}\right.$$ We now look at the boundary maps $$\begin{align*} D_n : \mathcal{Hom}_{\mathbb{Z} G} (P_\bullet, \mathbb{Z})_n &\rightarrow \mathcal{Hom}_{\mathbb{Z} G} (P_\bullet, \mathbb{Z})_{n - 1},\\ f &\mapsto d' \circ f - (-1)^n f \circ d, \end{align*}$$ where $d$ is the boundary map in $P_\bullet$ and $d'$ is the boundary map in $\mathbb{Z}$. It is immediate that $d' = 0$, since the resolution it acts on is just $$\cdots \xrightarrow{d'} 0 \xrightarrow{d'} 0 \xrightarrow{d'} 0 \xrightarrow{d'} \mathbb{Z}.$$ So the map is now $D_n (f) = (-1)^{n + 1} f \circ d$. When $n$ is odd, we get that $$\begin{align*} D_n (f) &= f \circ d_n,\\ &= f \circ (g - 1), \quad \text{since $n$ is odd},\\ &= f \circ g - f \circ 1,\\ &= f \circ 1 - f \circ 1, \quad \text{since $g$ acts by $1$ on $\mathbb{Z}$},\\ &= 0.\end{align*}$$ Similarly for $n$ even we get $$\begin{align*} D_n (f) &= (-1) f \circ d_n,\\ &= (-1) f \circ (1 + g + \cdots + g^{m - 1}), \quad \text{since $n$ is even},\\ &= -f \circ 1 - f \circ g - \cdots - f \circ g^{m - 1},\\ &= -f \circ 1 - f \circ 1 - \cdots - f \circ 1, \quad \text{since $g$ acts by $1$ on $\mathbb{Z}$},\\ &= -m f.\end{align*}$$ Which tells us that if $n$ is odd, $D_n$ is the $0$ map, and if $n$ is even, $D_n$ is multiplication by $-m$. We now end up with the following chain complex for $\mathcal{Hom}_{\mathbb{Z} G} (P_\bullet, \mathbb{Z} )$: $$\cdots \rightarrow 0 \rightarrow 0 \rightarrow \mathbb{Z} \xrightarrow{0} \mathbb{Z} \xrightarrow{-m} \mathbb{Z} \xrightarrow{0} \mathbb{Z} \xrightarrow{-m} \cdots.$$ To take the cohomology, we look at the cochain complex and cut off the negative degree entries: $$\mathbb{Z} \xrightarrow{0} \mathbb{Z} \xrightarrow{-m} \mathbb{Z} \xrightarrow{0} \mathbb{Z} \xrightarrow{-m} \cdots.$$ Taking the cohomology of this cochain complex gives us the result, $$H^* (\mathbb{Z} / m ; \mathbb{Z}) = \left\{ \begin{array}{l l} \mathbb{Z}, & * = 0,\\ 0, & * \text{ odd},\\ \mathbb{Z} / m, & * \text{ even}, * > 0. \end{array}\right.$$